This text is a translation of that of the Dutch PLN-NL, which is of a different design than most planispheres (which are round). The information below is meant to enable you to understand the planispheres better and to use them with more ease.
Astronomy
On a clear and dark night you can admire the starry sky. If you do so for a number of successive nights you will notice that you see the same groups of stars over and over again. These constellations don't change in relation to surrounding constellations, but are in a slightly different position compared to the situation the same time the night before. It appears as if all stars have moved a little to the east. In the course of this 'stargazing', you will notice that stars rise in the east, slowly move to the south (if you live in the northern hemisphere) or north (for those in the southern hemisphere) where they culminate, finally setting in the west, just as the Sun does.
The day
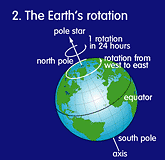
This cycle of stars rising, culminating and setting is caused by the Earth rotating on its axis, one rotation per 24 hours. This rotation is
anticlockwise (as seen from above the north pole). Or - to put it another way - the Earth rotates from
west to east (see illustration 2). So if you are standing on the Earth (which I assume you are!) you also move to the east. Moreover, you do this at an incredible speed: approximately 0.5 km/s at the equator! Because of our planet's eastward movement the Sun, the Moon, the planets and the stars appear (rise) in the east and disappear (set) in the west.
The year
As well as rotating on its axis the Earth also revolves around - or orbits - the Sun. It takes the Earth
365¼ days to do so, or one year. You can't do much with a quarter of a day (6 hrs). That is why once every four years we have a leap year with an extra (366th) day in the year: a leap day, on 29 February.
Otherwise, for the sake of convenience, a year has 365 days. Each complete day the Earth covers 1/365th part of its orbit. This results in the Sun changing its position against the distant stars (see illustration 3) moving from west to east. Thus, in the course of a year the Sun thus follows a predictable 'path', which you will find marked on both star charts. You won't see this happening, because the Sun is far too bright and outshines the other stars! However, you can see stars during a total solar eclipse, when the Sun hides behind the Moon for a few minutes and it gets dark in daytime.
The ecliptic
Because eclipses can only be seen along the Sun's path, this is known as theecliptic: the path of the eclipses. The ecliptic runs through twelve famous constellations: the constellations of the zodiac. You can find them on the planisphere. These constellations owe their reputation to the fact that they are 'visited' by the Sun every year. Only a few - e.g.
Gemini and
Leo - are really striking constellations.
Astrologers set great store by these ‘signs of the zodiac', although the actual position of the Sun has not corresponded with astrology for the last few thousand years. This is because the Earth's axis is wobbling, a process we call
precession (see below). Besides the Sun 'visits' thirteen constellations: after a week in
Scorpio the Sun can be found another three weeks in
Ophiuchus , the Snake Bearer! The Sun also doesn't neatly spend a month in each constellation of the zodiac. It varies from less than three weeks in
Cancer to six weeks in
Leo.
Solar day and sidereal day
Because the Sun continually moves to the east (about 1° per day) it gets behind relative to the stars. When the Sun rises at the same time as a certain star today, that star will rise shortly before the Sun tomorrow. A week later we will see the same star rise well before the Sun. Our daily life is organised around the solar day: at 12 o'clock (noon) the Sun culminates; 24 hours later the Sun is at exactly the same place in the sky! The sidereal day is equal to the time it takes the Earth to rotate once: 23 hours 56 minutes and 4 seconds. The sidereal day is thus 3 minutes and 56 seconds shorter than the solar day.
Our time
If our time is based upon the position of the Sun at noon, than time must be a very ‘local' phenomenon. After all, the Sun cannot culminate everywhere at the same time! In the past people indeed used ‘local time' everywhere. Every town had a sundial which was normally used to adjust the the church clocks (see our 'build-it-yourself' sundial!). It didn't matter that the next town had a different time, because life wasn't so fast. With the arrival of new techniques like the telegraph and the steam train, it became necessary to have a time for a larger area, a whole nation or at least a time zone. In the Second World War, when the Nazi's occupied most of Europe, they introduced one time for all of Western and Central Europe: Central European Time or CET. When the German troops left, this CET stayed. In Europe only the UK, Ireland and Portugal use a different time: Greenwich Mean Time (or GMT; it is the same as Universal Time - UT - which is used in science and for instance for space flights). The CET region is the largest time zone in the world.
The world is divided in 24 time zones (because a day is 24 hours). The centre
meridians of the standard time zones are
360° divided by 24 = 15° of longitude apart, with Greenwich as the zero point (the
prime meridian !). As the difference between to time zones is one hour, every degree of longitude is equal to 4 minutes in time.
For CET the centre meridian is at 15° east. We will use this as an example. As we have seen before, the Sun can not culminate everywhere in Europe at the same time. CET is correct at 15° east longitude, about the longitude of Prague and Vienna. In those places the Sun will indeed culminate (or be exactly in the south) at noon - 12.00 hrs. My home town Amersfoort, The Netherlands is situated at 5° east longitude. The difference with the 15° east meridian is 10°. The Sun will therefore culminate in Amersfoort 40 minutes later than it did at 15°, so at 12.40 h (when daylight saving time is used it will be even 13.40 h for the Sun to be exactly in the South).
The seasons
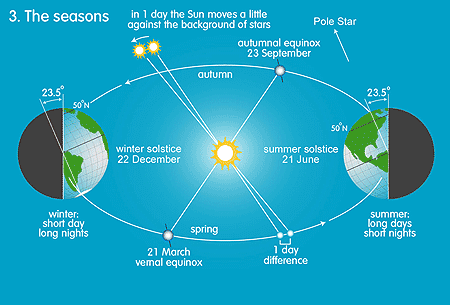
An Earth globe is always tilted on its stand. The reason for this is that the Earth's axis has a 23½° tilt with respect to the plane of its orbit around the Sun. This tilt causes the phenomenon of the seasons (see ill. 3).
In the summer the Sun is above the northern hemisphere, or to be more precise: above the tropic of Cancer, at 23½° N. We call this the summer solstice. At higher latitudes on 21 June the Sun rises early in the morning in the northeast, to travel in a long arc across the sky, culminating very high in the sky at noon, and setting late at night in the northwest. So people in these regions have long days and short nights! At the same time it is winter at the more southern latitudes in the southern hemisphere, with the Sun tracing only a small arc and reaching a modest height during culmination. The days there are short and the nights long. On 22 December, when the Sun is precisely above the tropic of Capricorn (23½° S) it is the winter solstice and the situation is exactly the other way round. On 21 March and 23 September the Sun is exactly above the equator and the days and nights are equally long. We call these the equinoxes.
Of course the situation in the tropics is not so extreme. If you are exactly on the equator, the only difference between summer and winter is the direction of the Sun. The Sun's altitude (the angular distance relative to the horizon) is 90 - 23½ = 66½° (over two thirds the distance from the horizon to the zenith!). For you on 21 June the Sun is 66½° above the north. On 22 December the Sun is 66½° above the southern horizon. For the rest of the year the Sun is even higher in the sky and on 21 March and 23 September the Sun will be overhead, able to illuminate the bottom of a well!
 Coordinates
Coordinates
All stars have their ‘fixed' place in the sky, but their distances vary greatly. Some are ‘close', like Sirius: 8.6 light years (ly). Others are much further away: Vega (Lyra) is 25 ly away, Rigel (Orion) 650 ly and Deneb (Cygnus) 1500 ly.
A light year is the distance covered in one year by light. The speed of light is the greatest speed we know: 300,000 km/s! So in one year light covers:
60 x 60 x 24 x 365.25 x 300,000 km, which is nearly 9500 billion km!
The farthest object we can see with the naked eye is the Andromeda Galaxy (M31), at 2.2 million ly. Distances, however, are not important for making a star chart.
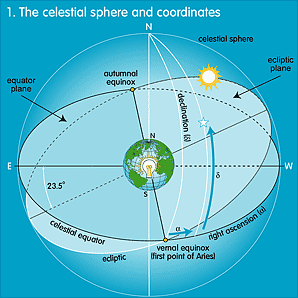
Suppose all stars are at exactly the same distance. We would than get a huge sphere of stars with the Earth in the centre! We call this the
celestial sphere (see ill. 1). To determine the position of a star, we need two coordinates, which correspond to latitude and longitude on Earth. Now suppose we have an enormously bright light in the centre of the Earth, projecting all points and circles we have 'drawn' on Earth. We would than get a
celestial equator ,
celestial poles and parallels and meridians. The astronomical equivalent of latitude is
declination , that of longitude
right ascension.
Right ascension
We have divided the celestial equator into 24
astronomical hours. Like the longitude used on the Earth's surface, we use
right ascension in astronomy, measured in those astronomical hours (and minutes and seconds). Degrees are also used: the celestial equator is than divided into 360° (1 hour = 15°). The planispheres only show hours and minutes: the outer circle of figures.
The
zero point in both systems is the same (0 hour = 0°), at the intersection of the ecliptic and the celestial equator (that is the black circle at a declination of 0°; see below). It is the position of the Sun on 21 March. This point is called the
vernal equinox, or the
point of Aries, because thousands of years ago it was situated in the constellation
Aries. It now lies in
Pisces and will enter Aquarius within a few hundred years. According to astrologers that will be the start of the Age of Aquarius.
There is another intersection of the ecliptic and the celestial equator: the autumnal equinox, on 23 September.
The planisphere allows you to very easily determine the right ascension of a star. Place the
red north-south line of the upper disc exactly over the centre of the star. Then read off the number of hours and minutes that the red line points out. Example: Capella is at 5 h and 14 min.
Declination
The
latitude we use to provide coordinates on the Earth's surface is equivalent to
declination on the celestial sphere. Declination is measured in degrees, from the
celestial equator. The celestial equator itself is at 0°, the celestial north pole at +90° and the celestial south pole at -90°. Examples: Capella has a declination of 46°, Arcturus 20° and Sirius -17°. The planisphere allows you to very easily determine the declination. For this, too, the red north-south line is used: the declination line (officially the
celestial meridian). This line runs from the Pole Star (+90°) and the zenith (the point exactly above your head) to the celestial south pole (-90°). The red line, that runs from west to east, intersects the declination line in this zenith. That east-west line is a help line to determine the altitude of a star above the horizon and in which direction you have to look to see a certain object. This line is a bit curved due to the projection that was used to design the star chart.
Illustration 1 shows the celestial coordinates system. We see the inclination of 23½° of the celestial equator with respect to the ecliptic plane (the plane in which most planets orbit the Sun). This inclination is caused by the tilt of the Earth's axis which, as we saw before, is 23½°.
Magnitude and star codes
The
brightness of a star is called the
magnitude. The magnitude scale was introduced by the Greek astronomer Hipparchus (2nd century BC). He divided the stars into six classes, from the 1st (the brightest stars) to the 6th magnitude (the dimmest, just visible stars). A star of the 1st magnitude is 100 times brighter than a star of the 6th magnitude. This means that a 1st magnitude star is 2½ times brighter than a 2nd magnitude star, and so forth.
Only when the telescope was invented (and used for astronomy!) could astronomers see stars that were dimmer than 6th magnitude. The dimmest objects that we can now see with our largest telescopes is around magnitude 30 (over 200 billion times dimmer than Sirius!). Very bright objectsn have a negative magnitude: Sirius -1.46; the full Moon -12.5; the Sun -26.8. The Sun is 20 billion times brighter than Sirius! With this information it is clear why you can't see any stars by daylight.
In the seventeenth century Johann Bayer introduced a system of
star codes. He gave the brightest star of a constellation the first letter of the Greek alphabet: ", the second in brightness: ß, and so forth. Most of the time this is still correct, but in Orion for example,
ß Orionis (Rigel) is brighter than
" Orionis (Betelgeuse)! Perhaps Betelgeuse was the brighter of the two then? Betelgeuse is a star nearing its death... Later, when telescopes grew bigger, astronomers had to use normal letters and cyphers as star codes.
The Pole Star and precession
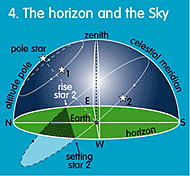
We never see more than half of the celestial sphere at a time: the other half is below the horizon! When you look at the stars it is as if you are standing in the centre of a hemisphere, just as in a projection planetarium. In all directions stars can be seen (see ill. 4). The celestial north pole is easy to find (unless you are on the southern hemisphere of course), because there is a famous star nearby: the Pole Star, or North Star, or Polaris. The Earth's axis points towards the celestial north pole, and thus towards that star, which is not very special besides being where it is. Polaris is quite similar to the Sun.
As the Earth spins on its axis, all the stars in the northern hemisphere sky seem to rotate around Polaris. Stars close to Polaris in the sky, like Cassiopeia and Ursa Major, are always visible above the horizon (well, when it is a clear night of course!). These are called
circumpolar stars and
circumpolar constellations. Those further away from Polaris rise in the east and set in the west like the Sun, and are only seen at certain times of the year. Use your planisphere to check this (see also ill. 4).
Polaris wasn't always a pole star. The Earth's axis wobbles slightly, like a top that you gave just a tiny push. One complete wobble of the Earth's axis takes about 26,000 years! We call this
precession . In the year 2000 BC the star Thuban (Draco, at ± 14 hrs right ascension) was ‘pole star' and in the year 14,000 Vega (Lyra) will be close to the celestial north pole.
Signposts in the Sky
It is very convenient that the Pole Star is precisely above the north now, for navigation at sea, or when you're lost in the fields. After all, if you know where north is, you also know the other directions!
But how can you find the Pole Star? You can use constellations as signposts to help find your way around the sky. The most important signpost to observers in the northern hemisphere is the saucepan-shaped part of Ursa Major (the Great Bear) that is called The Plough by the British and the Big Dipper by the Americans.
To find north, use the two stars on the edge of the bowl (Merak and Dubhe; see ill. 5) to locate the North Pole Star (Polaris; where the rivet is). The horizon directly below Polaris is due north.
The saucepan can be used to find more stars: follow the curve of the handle and you'll find Arcturus (Boötes) and if you let the 'pancake slip out of the pan' by following the line Megrez - Dubhe you'll reach Capella (Auriga)! Alcor/Mizar is a wonderful double star and a great eye test. Indian boys had to see both stars before they were allowed to go hunting with the adult warriors!
The elevation of the Pole Star above the northern horizon tells us another thing: it is equal to the latitude of your place of observation! For instance in Amersfoort, The Netherlands, the Pole Star is 52° above the horizon, so I live at 52° north. On the north pole the Pole Star is at 90° (in zenith); on the equator we see the Pole Star on the northern horizon: 0°.